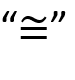Gentilissimi e, ovviamente, gentilissime,
dopo un tour de force, in concomitanza con il Tour de
France, e un’operazione all’anca, sono tornata a salutare i miei nipotini.
Per caso, non Domenico, ecco che il buon Jack No Sparrow chiede
informazioni sulla proprietà delle proporzioni detta “comporre” e la sua
viceversa detta “scomporre”.
Vediamo un poco l’esercizio proposto:
x : (5/4 – x) = 5/9 : 5/18
Il secondo termine della proporzione contiene una differenza:
(5/4 – x).
Il sottraendo della differenza è l’incognita. Applichiamo la
“proprietà viceversa”: “se c’è un meno, faccio il più”. In termini maggiormente
matematici, sommo ogni antecedente con il suo conseguente. Ecco cosa si
ottiene (MI RACCOMANDO LE PARENTESI a entrambi i conseguenti):
x : (x + 5/4 – x) = 5/9 : (5/9 + 5/18)
al secondo termine, ora, abbiamo una addizione algebrica. Possiamo
applicare la commutativa della addizione:
x : (5/4 +x -x) = 5/9 : (5/9 + 5/18)
nel secondo termine, alla frazione 5/4 è stato aggiunto e
sottratto lo stesso numero x. Il risultato, tra parentesi, sarà proprio 5/4
x : 5/4 = 5/9 : (5/9 + 5/18)
Risolviamo l’addizione al quarto termine:
x : 5/4 = 5/9 : (15/18)
Riduciamo ai minimi termini 15/18
X : 5/4 = 5/9 : 5/6
Applichiamo la proprietà fondamentale delle proporzioni: “prodotto
estremi uguale prodotto medi”
5/6 x = (5/4)(5/9)
5/6 x = 25/36
Come dicono le Vostre nonne: “Se a sinistra ho una
moltiplicazione, a destra devo fare la divisione, e viceversa”
x = 25/36 : 5/6
“Cosmizzo il divisore 5/6” (e se non sapete chi è Cosmo,
dovrete comperarVi un cappellino rosa!)
x = (25/36) (6/5)
semplifico la moltiplicazione
x = 5/6
Ed ora tocca a Voi! Se volete potrete inviare le Vostre
soluzioni come commento:
a)
(3/5 – x )
: x = 2/3 : 1/10
b)
7/4 : 3/2 = (3/4 + x) : x
NR, Nonna Rifatta (all’anca!)