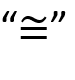pi greco

IL PI GRECO ϖ

COS’E’ IL PI GRECO ϖ?

1)      E’ UN NUMERO ASSOLUTO DECIMALE IRRAZIONALE TRASCENDENTE APERIODICO

N-A-D-I-T-A

NUMERO: 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679… CIRCA

ASSOLUTO: E’ “PROPRIO QUELLO E NON UN ALTRO”, QUINDI “E’ PRECISO!”, “E’ COSTANTE”!

DECIMALE: HA LA VIRGOLA E NON E’ UN INTERO

IRRAZIONALE: NON E’ UNA FRAZIONE

TRASCENDENTE: NON SI TROVA COME RISULTATO DI UNA EQUAZIONE CON COEFFICIENTI RAZIONALI

APERIODICO: NON HA ALCUN PERIODO

2)    E’ IL RAPPORTO TRA CIRCONFERENZA E DIAMETRO.

OPPURE

E’ IL RAPPORTO TRA AREA DEL CERCHIO E RADICE QUADRATA DEL RAGGIO.

QUINDI

ϖ = C/d          OPPURE       ϖ = Ac/√r

DALLA DEFINIZIONE DI PI GRECO POSSIAMO RICAVARE LE FORMULE PRINCIPALI DEL CERCHIO E DELLA CIRCONFERENZA:

LUNGHEZZA DELLA CIRCONFERENZA

C = d ϖ u  OPPURE   C = 2 r ϖ  u

INFATTI IL DIAMETRO E’ IL DOPPIO DEL RAGGIO (d = 2 r)

AREA DEL CERCHIO

Ac = r² ϖ u²

OPPURE 

Ac = (d/2)² ϖ u² QUESTA FORMULA SI USA RARAMENTE

APPROSSIMAZIONI DI PI GRECO E LORO UTILIZZO

ϖ NON E’ 3,14 !!!

APPROSSIMAZIONE ϖ ~	UTILIZZO
3	NEL MONDO ANTICO E NELLA BIBBIA
3,1	PER CALCOLI VELOCI, SENZA CALCOLATRICE, O SE IL RAGGIO E’ MULTIPLO DI 10
3,14	SE IL RAGGIO O IL DIAMETRO SONO MULTIPLI DI 100
22/7	SE IL RAGGIO O IL DIAMETRO E’ UN MULTIPLO DI 7 M(7)
3,14159	SE SI HA LA CALCOLATRICE, IN ARCHITETTURA O IN INGEGNERIA
223/71	APPROSSIMAZIONE DI ARCHIMEDE
355/113	APPROSSIMAZIONE DI ZU CHONGZHI, NELLA CINA ANTICA

^{SE SI APPROSSIMA SI DEVE METTERE SEMPRE IL SIMBOLO “~”}

^{VI LASCIO ANCHE UNA ESPRESSIONE CHE, PER ME, E’ “BELLA”}

SCRITTA IN UN ALTRO MODO (PIU’ FACILE)

 ϖ = 4(+1/1 -1/3 + 1/5 – 1/7 + 1/9 – 1/11 + …)

1)               SI METTE ϖ = 4 “PER”;

2)               SI APRE UNA TONDA;

3)               SI SCRIVONO LE UNITA’ FRAZIONARIE CON DENOMINATORE DISPARI

4)               SI ALTERNANO I SEGNI PIU’ E MENO, PARTENDO DAL PIU’

5)               SI METTONO I TRE PUNTINI PER DIRE CHE SI PUO’ PROSEGUIRE ALL’INFINITO

TALE MODALITA’ DI ESPRIMERE IL PI GRECO E’ DETTA

FORMULA DI MADHAVA-LEIBNIZ

1° COMPITO

DISEGNA UN CERCHIO DI CENTRO O E RAGGIO 2 cm. DISEGNA IL RAGGIO OA. DISEGNA IL DIAMETRO AB. DAL PUNTO A, TRACCIA UN SEGMENTO AC PERPENDICOLARE AL RAGGIO OA E DI LUNGHEZZA PARI AL DIAMETRO. CALCOLA LA LUNGHEZZA DEL SEGMENTO BC. NON APPROSSIMARE!

2° COMPITO

ESEMPIO:

SIA DATO UN CERCHIO DI RAGGIO OA CHE MISURA 13 CM. CALCOLA LA MISURA DELLA CIRCONFERENZA E L’AREA DEL CERCHIO.

F-A-S-C-R-U

C = 2 r ϖ u                  Ac = r² ϖ u²

C = 2 OA ϖ cm             Ac = OA² ϖ cm²

C = 2 · 13 ϖ cm            Ac = 13² ϖ cm²

C = 26 ϖ cm                 Ac = 169 ϖ cm²

NON SONO NEI CASI DI APPROSSIMAZIONE INDICATI IN TABELLA, QUINDI

NON APPROSSIMO PI GRECO!!!

ED ORA A VOI!

SIA DATO UN CERCHIO DI RAGGIO OA CHE MISURA 7 CM. CALCOLA LA MISURA DELLA CIRCONFERENZA E L’AREA DEL CERCHIO.

(SONO NEI CASI INDICATI IN TABELLA? SE SI’, QUALE APPROSSIMAZIONE DOVRO’ USARE?)

RICORDA DI NON METTERE IL SEGNO “=” QUANDO APPROSSIMI, 

MA METTI IL SEGNO “~” 

O 

       

NR, Nonna Raggio (forse più circonferenza che raggio!)

m.c.m. (primo metodo per elencazione)

m.c.m.

COSA SIGNIFICA m.c.m.?

m. = minimo, cioè?  “Il minore”

c. = comune, cioè? “Che vale per tutti i numeri considerati”

m. = multiplo, cioè? “presente nella tabellina considerata”

Quindi m.c.m. è 

IL MINORE NUMERO PRESENTE NELLE TABELLINE E VALIDO PER TUTTI I NUMERI CONSIDERATI.

Come si trova?

QUESTA VOLTA NON semplicemente. Il procedimento è complesso.

1)    Si fanno gli elenchi dei MULTIPLI di ogni numero. IN COLONNA AUSILIARIA, MI RACCOMANDO

PER TROVARE m.c.m. DEVO PROSEGUIRE SINO A QUANDO TROVO UN NUMERO CHE SIA LO STESSO NELLE TABELLINE CONSIDERATE!!!

Usate pure la calcolatrice!

METTETE, ANCHE IN COLONNA AUSILIARIA, I TRE PUNTINI!

I MULTIPLI DI UN NUMERO SONO INFINITI!!!

2)    Si osservano i numeri che sono uguali in TUTTI gli elenchi

3)    Si considera il numero MINORE

4)    Si scrive il risultato, CON I NUMERI DI PARTENZA INDICATI IN ORDINE CRESCENTE

Facciamo un esempio: qual è il m.c.m. tra 20 e 24?

(I NUMERI ASSEGNATI SONO IN ORDINE CRESCENTE?)

SE NON LO SONO, DEVO ORDINARE I NUMERI ASSEGNATI, MI RACCOMANDO!

1)    Facciamo gli elenchi

M(20) = [20;40;60;80;100;120; …]

C.A. 20X1=20     20X2=40    20X3=60    20X4=80    20X5=100 20X6=120 …

M(24) = [24; 48; 72; 96; 120; 144; …]

C.A. 24X1=24     24X2=48    24X3=72    24x4=96    24x5=120 …

2)    Cerchiamo quelli uguali nei due elenchi

HO TROVATO UN NUMERO CHE SIA LO STESSO NELLE DUE TABELLINE?

CERTO!               E’ IL 120.

E’ IL PRIMO NUMERO “UGUALE” E PRESENTE IN TUTTE LE TABELLINE CONSIDERATE?

CERTO!

QUINDI TUTTI I M(120) SARANNO PRESENTI IN ENTRAMBE LE TABELLINE CONSIDERATE

FACCIO LA C.A. (“VERSIONE NORMALE”) PER M(120)

C.A. 120X1=120          120X2=240         120X3=360         …

MI RACCOMANDO, QUANDO SI CALCOLANO I MULTIPLI, SEMPRE I TRE PUNTINI

M(120) = [120;240;360; …]

3)    Qual è il minoore?

OVVIAMENTE 120

4)    m.c.m. (20;24) = 120   (I NUMERI ASSEGNATI SONO IN ORDINE CRESCENTE?)

COMPITO

·       TROVA m.c.m. TRA I NUMERI 8 E 6

(I NUMERI ASSEGNATI SONO IN ORDINE CRESCENTE?)

·       TROVA m.c.m. TRA I NUMERI 12 E 16

FACOLTATIVO MISTERO MISTERIOSO

PERCHE’ GIULIO CESARE POTEVA ESSERE, IN DISTOPIA, A BORDO DEL DIRIGIBILE ZEPPELIN LZ 1?

PER “DISTOPIA” SI INTENDE UN FUTURO POSSIBILE, MA “NEGATIVO” NON PROPRIAMENTE FELICE, PER IL PERSONAGGIO, IN QUESTO CASO GIULIO CESARE, IN QUESTIONE.

RISPOSTE AL NONNO

Gentilissimi e gentilissime, nel presente post si correggono alcune risposte a domande teoriche di statistica.
Il rispondente è il Nonno non so la matematica.
E se non sapete dove sono nascoste le domande, e, tuttavia, sono ben visibili, inviate pure richiesta in merito.
Sappiate che le Vostre Nonne potrebbero farne altre. Non crediate che, rispondendo a queste, si possa rispondere a tutte quelle possibili in merito.
Procediamo con le risposte al Nonno:

11) In ambito scientifico, in particolare naturalistico e mineralogico
18) è un areogramma che serve per ....
19) è il valore che divide esattamente a metà il campione
21) eliminando, dopo averli ordinati, contemporaneamente i valori estremi sino a quando ...
23) curva "a sigma", o, meglio, "sigmoidale"

Certo che questo Nonno, per non sapere la matematica, non è per nulla male!!!

NR, Nonna Rispondente

numeri divisibili per 11 (cl.1) - un trucco da poco

Gentilissime e gentilissimi,

come possiamo “trasformare” un numero NON divisibile per 11 in un numero che si possa dividere per 11?

Ovviamente con “un trucco”.

Facciamo un esempio:

consideriamo il numero 39874903

·         Trascriviamo il numero, separandone le cifre:

3    9     8    7    4    9    0     3

·         Evidenziamo le cifre in “posizione dispari”, ossia unità, centinaia, decine di migliaia, …

3    9     8    7    4    9    0     3

·         Evidenziamo, in altro modo, le cifre in “posizione pari”, ossia decine, unità di migliaia, centinaia di migliaia, …

3    9     8    7    4    9    0     3

·         Sommiamo le cifre evidenziate in rosso:

9 + 7 + 9 + 3 = 28

·         Sommiamo le cifre evidenziate in verde:

3 + 8 + 4 + 0 = 15

·         Consideriamo quale delle due somme così trovate sia maggiore. In questo caso 28 > 15. Effettuiamo la sottrazione possibile in N:

28 – 15 = 13

·         Consideriamo ora la differenza così trovata. In questo caso abbiamo ottenuto un numero che non è NÉ ZERO (0) E, NEPPURE, UN MULTIPLO DI 11 (M(11)). Se avviene questo, allora significa che il numero di partenza NON E’ DIVISIBILE PER 11.

·         Come facciamo a “trasformare” il numero di partenza in un numero divisibile per 11?

Dovremmo fare in modo che il numero in verde, ossia il sottraendo, sia un poco “più grande”. Di quanto dovremmo aumentare il numero verde?

Ragioniamo: se ho ottenuto una differenza di 13, e dovevamo ottenere una differenza di 11, significa che devo aumentare di 2!

Se così fosse otterremmo 28-17=11

Come volevamo ad inizio procedimento!

Si tratta di “aggiungere” una cifra 2 tra quelle in verde! Ecco nuovamente il numero di partenza:

3    9     8    7    4    9    0     3

Dove possiamo “aggiungere” una cifra in verde? In questo caso, sicuramente, NON a sinistra. Altrimenti ci troveremmo con due cifre in verde consecutive!

Se, invece, “aggiungiamo” la cifra 2 a destra, avremmo rispettato il procedimento. Scriviamo il 2 a destra, come vedete sotto:

3    9     8    7    4    9    0     3    2

·         Ora, se volete, potete ricontrollare per conto Vostro!

NR, Nonna Ragionante, almeno per ora!

correzione compiti - numeri divisibili per 3; 3 exp 2; (2x3)

Gentilissime e gentilissimi,

ancora il Nostro, e Vostro, Suresh ha inviato per correzione altri esercizi.

La Nonna, oltre a lavorare a punto-croce, che non è “giocare a tris”, proverà a correggere, per quanto possibile.

La consegna era la seguente, valida per tutti gli esercizi:

Scrivi 5 numeri con 4 cifre diverse, che siano divisibili per …

Ovviamente, per i numeri divisibili per 100, …ooops (2 ² x 5 ²), ciò non è possibile.

Vediamo gli elaborati dei nipotini:

1) 

 

Direi nulla da eccepire! Nice work! I due elaborati sono corretti!

2) 

In questo elaborato si nota un errore molto comune tra i giovanotti.

Tra il numero scelto, corretto in quasi tutti i casi, e la costruzione del Mod. si nota il segno “=”.

Questo significherebbe che, come è scritto, 3465 = 18

Ovviamente questo è un errore. Probabilmente il nipotino voleva indicare altro.

Come avrebbe dovuto scrivere?

3465                                      Mod.  3+4+6+5=18         Mod. 1+8=9        Mod. (3465) = [9]

Nella consegna è scritto “numeri dispari divisibili per 9”. Ma 9 NON è un numero primo! Bisognava scrivere “divisibili per 3 ²”.

Si nota, inoltre, una imprecisione: il secondo numero scelto, tra quelli divisibili per 6, sarebbe stato mooolto meglio scrivere (2x3), è 5258. Il calcolo del Mod., tuttavia, utilizza il numero corretto 5238. Probabilmente un errore di copiatura o un refuso.

3) 

Vediamo un poco!

A ) I 5 numeri divisibili per 3: “un numero è divisibile per 3 se ha mod. [3]; [6]; [9]”.

Quindi, ogni volta, dobbiamo pure calcolare il mod.!

Per il numero 7529         mod.  7+5+2+9=23       2+3=5    Mod. (7529) = [5] 

Quindi NON è divisibile per 3

Per il numero 3265      mod.   3+2+6+5= 16       1+6=7   Mod. (3265) = [7] 

Quindi NON è divisibile per 3

Per il numero 9871      mod.     9+8+7+1=26     2+6=8     Mod.(9871) = [8]  

Quindi NON è divisibile per 3

B) I 5 numeri divisibili per 9 (Aaaargh! Si scrive 3 ²!): 

“un numero è divisibile per 3 ² se ha Mod. [9]”

Per il numero 4683     mod. 4+6+8+3=21    2+1=3    Mod.(4683) = [3]  

Quindi NON è divisibile per 3 ²

Per il numero 1257     mod.   1+2+5+7=15   1+5=6   Mod.(1257) = [6] 

Quindi NON è divisibile per 3 ²

Per il numero 5371    mod.  5+3+7+1=16   1+6=7   Mod.(5371) = [7] 

Quindi NON è divisibile per 3 ²

Per il numero 3689   mod.   3+6+8+9=26   2+6=8   Mod.(3689) = [8] 

Quindi NON è divisibile per 3 ²

Per il numero 7365    mod.  7+3+6+5=21    2+1=3   Mod.(7365) = [3] 

Quindi NON è divisibile per 3 ²

C) un’unica imprecisione. NON si deve scrivere  “divisibili per 6”, in quanto 6 NON è un numero primo.

Moooolto meglio scrivere “divisibili per (2x3)”.

4) 

 - numeri divisibili per 3: una sola imprecisione: in TUTTI i numeri le 4 cifre dovevano essere differenti. Nel numero 3333, ovviamente, non è stata rispettata tale richiesta.

- numeri divisibili per 9!!!! Ma non ho già detto più volte che 9 NON è un numero primo?

Si deve scrivere “3 ² “.

Cosa dire? Diamo per scontato che il primo numero sia 5175 e non 5125, visti i numeri successivi. Ma le 4 cifre dovevano essere diverse. Per il resto sono tutti numeri divisibili per 3 ² . (Però con poca fantasia!)

-          numeri divisibili per 6!!!! Ma non si doveva scrivere (2x3)? 6 NON è un numero primo!

Se un numero è divisibile per (2x3) soddisferà ad entrambi i criteri, sia del 2, cioè sarà un numero pari, sia del 3, ossia avrà mod. o 3 o 6 o 9. Nessuno dei numeri scritti è pari! Quindi nessuno sarà divisibile per (2x3)! Oltre a ciò nello stesso numero non tutte le cifre sono diverse! Una Nonna direbbe: “Pallino rosso!”, ossia, traduco dal nonnese, “esercizio da rifare”.

Per evitare post eccessivamente lunghi, per ora, e solo per ora, mi fermo qui!

NR, Nonna ripetitiva